量子力学中的波

《波的科普》系列文章之（四）

在量子力学中，波有更丰富的物理内涵。

在微观世界中，人们宏观世界的经验不再适用，量子力学便派上了用场。许多人都知道，光有波粒二象性。实际上，电磁波都具有粒子性，具有量子化的能量，比如之前我们用子弹和雨滴形容X射线和无线电波的单份能量。

1923年，德布罗意（Louis Victor de Broglie，法国著名理论物理学家，创立了波动力学和物质波理论，量子力学的奠基人之一）将波粒二象性的概念推广到有静止质量的实物粒子上，提出“任 何物体都伴随有波”，质量越大，波长越小。这种与实物粒子相对应的波称为德布罗意波或者物质波，以区分机械波和电磁波。

单电子波动实验证明了物质波存在。如果把做杨氏双缝干涉实验（见下图）的光源换成电子源，并且让电子一个个地单独发射，时间积累足够长，干涉图样也 会出现。干涉图样的出现证明了电子的波动性，单个电子一次次通过是为了证明了波动性来自电子本身，而不是来自一群电子的集合体。如果作为一个经典的粒子， 比如一个足球，它只能从两个缝隙之一通过。而实验上的一个电子既从狭缝S1通过，又从狭缝S2通过，自己跟自己形成干涉，这样的行为只有波才能做到。

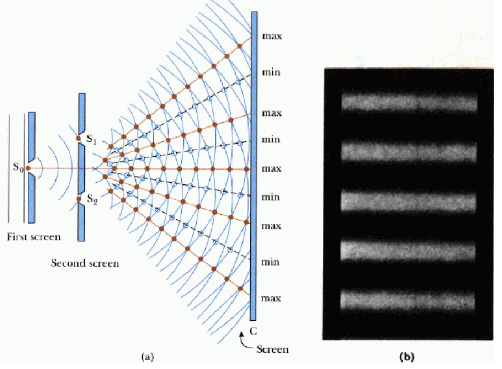
杨氏双缝实验示意图：当一个波通过两个缝S1和S2时，在远处的平板上形成明暗相间的条纹，这是波动性的重要证据。

在上面的电子衍射实验中，我们无法预测具体某个电子通过是S1还是S2，这跟经典物理的常识不一致。在经典物理中，“上帝不掷骰子”，只要给定单个 粒子的初始条件，粒子的轨迹就被确定下来了。为了理解这些经典力学无法解释的现象，量子力学用波函数来描述客观世界，对应的基本方程不是牛顿方程，而是薛 定谔方程。波函数的大小跟粒子出现的概率是对应的。电子在原子核的外部，我们常常看到类似下面左边的图片，图片中电子似乎是环绕着质子和中子运动，仿佛质 子和中子是太阳，电子是类似地球的行星。电子如果按照一个非直线的轨迹运动，需要对外发射电磁波，也就是释放能量，那么最终原子的结构就无法稳定，因为电 子的能量在不断减少。实际上电子在原子核外并没有固定的轨迹，而是形成一定的概率分布，如下面右图所示。我们无法“跟踪”微观粒子的行动，我们只能知道在 某一个时间点，它在某一个空间点出现的可能性有多大。

左图：经典力学下电子轨迹示意图，这样的图过时了七八十年了。右图：实际电子在氢外的概率分布，颜色越黑（点越密集）代表电子出现的概率越大。六个图代表几种电子可能出现的模式。

再举一个波函数的例子：无限深方势阱中的 粒子。这是量子力学教科书里面几乎必然出现的经典范例。假如我们有一个非常非常深的直长深坑，坑里有一个球，球一开始在蹦达，足够长的时间之后，这个球肯 定是静止在坑底部的某一个位置。这个我们熟悉的结果隐藏着经典力学几个在量子力学中不再成立的事情：连续能量、零基态能、确定位置、静止。量子力学中，薛 定谔方程最后解出来的答案里，能量只能是固定的一组数值，粒子无法像球一样在空间中连续变化高度（相当于连续变化重力势能），只能从满足波函数的一个能量 值变到另一个能量值，这时候我们说系统的能量是量子化的，这也是量子力学这个叫法的来由。在满足薛定谔方程的解中，最低能量并不是零，这个能量称为零点 能，与之相反，球可以出现在重力势能最低的地方。粒子在任意一个可能的能量中，它无法确定在坑中具体的位置，它可能在坑的偏左，也可能在偏右，也可能在中 间。不仅粒子出现在各个位置的概率不是均匀的，各个能级中粒子的可能出现概率分布也是不同的。最后，量子力学中没有静止的概念，非零的能量暗示着非零的动 量，暗示着没有不动的粒子。

量子力学里没有静止的粒子也意味着没有“静止的物质波”，波总是占据着空间中一定的位置分布，这个与经典粒子的区别正是微观粒子波动性的表现。我们 也可以从量子力学中出名的不确定度关系中定性推导出无限深方势阱中粒子的结果：因为空间的最大不确定等于势阱的宽度，那么动量与宽度成反比，但为一有限 值，所以能量不可能为零。这类可以由物理常识快速得到答案的问题是一些老师面试研究生时的最爱。这个问题接下来的问法可以问势阱宽度突然增大或者减少一半 时里面粒子的演化情况，也可以问如何从量子情况演化到经典情况。

经典力学符合人们的直觉，量子力学违背人们的直觉，这两者看似矛盾，其实在各自的应用领域都是正确的；矛盾的地方只是它们应用在不同的条件和场合。 相对论与经典力学的关系中，光速为一个关键参数：速度远小于光速时，可以不使用相对论。量子力学与经典力学的关系中，这个参数是普兰克常数，当一个系统有 普兰克常数量纲的数远大于6.63E-34时，可以不使用量子力学，这个量纲在经典力学中跟[长度]*[动量]、或者[时间]*[能量]一致（其实就是角 动量的单位）。用我们熟悉的[时间]和[能量]为例子，老一辈人常见的摆钟中，摆动的周期是秒，总能量是焦耳或者10焦耳量级的，比普兰克常数大了三十多 的数量级，不需要考虑量子力学。之前提到的无限深方势阱，低能级的动量跟[普兰克常数/势阱宽度]相关，所以再乘以一个[长度]时，需要考虑量子力学。当 能级逐渐增加时（薛定谔方程对这个问题有无穷个解），动量渐渐增加，于是经典力学就逐渐占据了主导地位。我们生活经验中的许多事物，角动量这个单位的数值 远大于普兰克常数，所以我们的直觉跟经典力学一致。

量子力学包含的内容太多，在这里我无法介绍得比较全面，也不想介绍得全面，这本来就不是几页纸能展开的事情。量子力学跟我们日常生活其实关系很大， 我们正在盯着的电脑或者手机，核心的技术来自于半导体，而半导体物理就是建立在量子力学之上的。百年前量子力学，一百五十年前的电动力学，本该是人类所共 同拥有的财富，可是现在还有“想像力丰富”的人幻想以太的存在，还有人买所谓的防辐射服。